玻璃幕墙挂钩式开启窗五金系统安全性分析-

玻璃幕墙挂钩式开启窗五金系统安全性分析

幕墙开启窗在日常使用过程中，五金系统故障已成为常见的质量缺陷，由此引发的开启窗整体脱落将严重影响公共安全。本文对挂钩式开启窗五金系统安全性进行有限元模拟计算，分析不同工况条件下的五金系统配件对开启窗整体安全性的影响，并对提升开启窗的安全性提出一些具体建议。本文可为玻璃幕墙开启窗的设计、安装以及使用维护提供一定的参考。

0 引言

玻璃幕墙开启窗常见工程质量问题主要有：玻璃外片脱落、开启窗整体脱落、五金系统故障等。在单元式玻璃幕墙常采用的挂钩式开启窗出现安全性问题的频率较高。其常见的破坏形式有两种：一是开启窗型材角部破坏、另一是开启窗脱钩造成的整体脱落。某挂钩式玻璃幕墙开启窗整体脱落的事故现场见图1、图2。

经事后调查分析，发生开启窗脱落的主要原因是，事发前施工现场未正常锁闭开启窗，在强风反复作用下，开启窗风撑和窗扇连接失效，失去了风撑的限位作用，开启扇顶部与横梁反复撞击导致型材组角部位断裂，从而导致开启窗整体脱落。所以为了保证挂钩式开启窗的安全，应做好开启窗五金系统的结构设计、控制好施工安装质量以及注意平时使用维护等几方面工作。

本文通过对挂钩式开启窗五金系统进行有限元分析，比较不同五金配置对开启窗安全性能的影响，进而为开启窗的设计、施工提供一定的参考。

1 计算模型

计算模型主要分析在开启状态下的五金系统主要受力部件（包括限位器、风撑），在设计风荷载和开启窗自重荷载作用下的力学性能是否满足规范和设计要求。

1.1模型材料参数

开启窗各部分材料如下：窗扇型材为铝合金，内部镶嵌中空玻璃；上部限位器为铝合金材料，撑挡为不锈钢材料。材料的物理参数见表1。

表1 材料参数

材料名称

弹性模量(GPa)

泊松比

密度(kg/m³)

屈服强度(MPa)

极限抗拉强度(MPa)

铝合金

68.9

0.33

2700

55.2

235

玻璃

0.25

2600

不锈钢

200

0.29

7900

310

620

1.2计算工况

为了完整分析结构的安全性及稳定性，结构计算工况见表2。

表2计算工况

工况编号

工况描述

说明

一

限位器和风撑正常工作

风撑限位器均正确安装

二

仅限位器正常工作

风撑损坏

三

限位器正常工作，仅一侧风撑正常工作

一侧风撑损坏

各工况下模型的计算方法为先整体，后局部的计算方法。首先，先对整个开启窗模型进行分析，采用弹性方法进行计算，将重力和设计风荷载施加在模型受力面上，计算出各约束处的约束反力。然后，建立限位器、撑挡扇上部件和框上部件精细的有限元模型，并将整体模型所得的约束反力作为荷载精细有限元模型上，进行弹塑性分析。最后，根据弹塑性有限分析结果评估整个模型的承载能力和安全性。下面具体分析每一工况下开启窗的五金系统主要受力部件的承载能力。

2 有限元分析结果

2.1 工况一：撑挡及限位器均正常工作

整体模型包括：窗扇（含玻璃）、上部限位器、顶部挂钩以及窗框与窗扇间连接的撑挡。整体模型见图3。

模型采用映射网格划分方法，划分之后总计15770个单元。对于主体模型单元采用壳单元进行模拟，对于下部两边的撑挡部件采用线单元进行模拟。模型建立时沿短边自左向右布置为X正方向，长边方向自下向上为Y正方向，垂直于玻璃面并指向窗外为Z正方向。模型建立完成后，对模型施加边界约束条件。针对模型的实际工作状态，分别对撑挡支撑杆末端、上部限位器和顶部挂钩三处施加约束。 1）开启窗约束反力

分析在风荷载2.19kPa和重力荷载条件下，各个约束端全部正常工作时，整体模型的各个约束处的力的大小。通过计算可得，整体模型在工况一下得出的约束反力见表3。

表3整体模型约束反力

约束反力

反力值/kN

上部限位器反力

1.67

下端撑挡支撑杆Y向反力

1.28

下端撑挡支撑杆Z向反力

2.11

将得到的约束反力加在撑挡扇上部件、框上部件及限位器模型上，并对其进行弹塑性分析，从而判断各个约束部位的工作状况。 2）限位器分析整体模型采用自由划分的方法划分网格，共4000个单元，实体部分采用实体单元。对模型上的三个固定螺丝孔施加约束，作为模型的约束条件，将之前所得限位器底端承受的荷载加载到限位器下部突出处。考虑到限位器并非下部整体受力，故仅在下部一半长度上的单元结点上施加荷载，模拟较为真实的限位器与开启窗的接触情况。模型建立完毕，采用弹塑性分析方法分析模型受力后的变形与应力状况。计算结果分位移向量及等效塑性应力，分别如图4、图5所示。

由计算结果可知，限位器的位移主要发生在端部受力部分，最大位移为0.46mm。从应力云图上可以看出，荷载作用下，绝大部分区域处在弹性范围内，较大的塑性应力仅发生在力作用部位小范围内，塑性应力发展区域约占宽度的1/2，且没有贯通。因此，限位器是安全的。 3）撑挡扇上部件分析

整体模型采用自由划分的方法划分网格，共224个单元，实体部分采用壳平面单元。对模型上的两个固定螺丝孔施加约束，作为模型的约束条件，将之前所得撑挡支撑杆末端的荷载加载于下部连接孔处。考虑到连接孔并非全孔受力，故仅在与撑挡支撑杆相接触的半圆区域结点上施加荷载，以此来模拟较为真实的撑挡扇上部件与窗扇的接触情况。

模型建立完毕，采用弹塑性分析方法分析模型受力后的变形与应力状况。计算结果分位移向量及等效塑性应力，分别如图6、图7所示。从位移云图可以看出，位移主要集中在受力螺孔周围，并且距离约束螺孔越远位移越大，最大位移0.065mm。从塑性等效应力云图中可以看出荷载作用下，绝大部分区域处在弹性范围内，较大的塑性应力仅发生在中间螺孔周边区域的极小范围内，最大值为312MPa，且没有贯通。所以可以得出结论：撑挡扇上部件也是安全的。

4）撑挡框上部件分析

主体底板模型采用自由划分的方法划分网格，两边的肋板及挡板采用映射划分的方法，划分完成后共2993个单元，实体部分采用壳平面单元。对模型上的两个固定螺丝孔部分区域施加约束，将实际中受拉力作用区域的约束放松，以此作为模型的约束条件，将之前所得撑挡支撑杆承受的荷载分别施加到撑挡框上部件挡块上和撑挡框上部件右侧与实际连接滑块长度相等的单元结点上，以此来模拟撑挡框上部件与撑挡支撑杆的接触情况。

模型建立完毕，采用弹塑性大变形分析方法分析模型受力后的变形与应力状况。计算结果分位移向量及等效塑性应力，最终一步计算后所得结果分别如图8、图9所示。

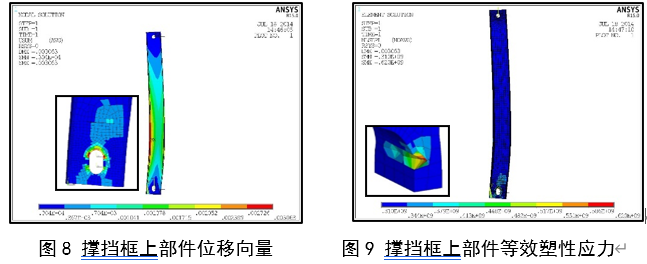
从位移向量云图可以看出，位移主要发生在受力位置边缘及其相对的肋板边缘，呈受力弯曲形状，位移向两边减小，最大位移为3.063mm。再观察塑性等效应力云图，可以看出荷载作用下，绝大部分区域处在弹性范围内，较大的塑性应力仅发生在下部约束螺孔周边区域的范围内，并且塑性应力区域向上发展，大部分区域塑性应力较小，局部小范围有集中的较大应力，但没有贯通，所以撑挡框上部件也是安全的。 5）结果分析

由各个构件的弹塑性分析结果可知，当上部两侧限位器和下部两侧撑挡均正常工作情况下，各个构件的应力并未超过极限抗拉强度，虽在局部出现塑性应力区，但应力区并未贯通，且应力没有达到极限强度，因此，整体结构是安全的。

2.2工况二：仅有上部限位器正常工作

尽管结构安装限位器之后对结构的整体安全性及稳定性均有改善，但是在实际服役过程中，上部的限位器与下部的撑挡基本上不能实现同时发挥作用，这也就导致了破坏的产生也不可能是同时的。因此有必要分析当下部的两处撑挡发生破坏后，仅有上部的限位器继续服役时结构的整体情况。

1）仅有上部限位器工况下开启窗整体模型的约束反力

分析在实际风荷载和重力作用下，仅有上部限位器约束时，整体模型约束力的大小。通过计算可得，整体模型在下端撑挡支撑杆的约束处产生的限位器约束力为23.43kN，此力通过窗框上部一处突出块体施加在窗框上，进而对开启窗模型施以反力。

将得到的约束反力加在限位器模型上，并对其进行弹塑性分析，从而判断各个约束部位的工作状况。

2）限位器分析

此处的力学分析模型与之前相同，仅在荷载大小上发生变化。采用弹塑性方法进行计算，采用分级加载，共分10级，当荷载加载到第2步时，计算不收敛。第1步的计算结果如图10、11图所示。

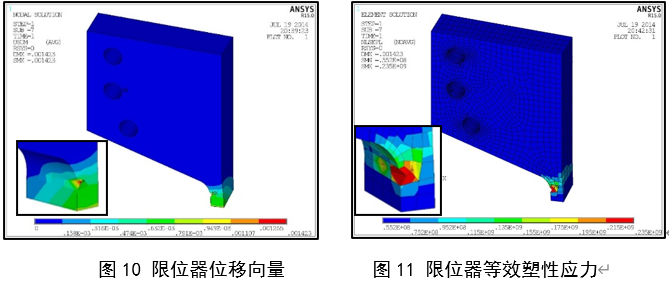
位移向量云图中最大位移1.423mm，主要集中在限位器与窗体接触部位的边缘，极易导致二者之间发生脱离；塑性等效应力云图中可以看出在工况二状态下，限位器底部边缘地区极易出现塑性屈服，当其屈服破坏后，限位器便会丧失约束能力，进而导致开启窗模型整体破坏。

3）结果分析

经过以上计算可以发现，当下部撑挡失效或由于安装原因而无法正常工作、或者下部撑挡先后发生破坏时，整个开启窗模型的稳定性则完全由上部的两侧限位器来维持。经计算发现，限位器底部边缘极易发生屈服破坏，产生塑性变形。一方面由于限位器自身强度不足产生破坏，导致限位器自身无法继续约束开启窗；另一方面当塑性变形增大到一定程度时，限位器与开启窗之间的接触变得极不牢靠，极易发生脱离，从而丧失约束能力。经过以上计算分析，表明了结构已经完全无法继续服役了。又因为总荷载为2.34kN，所以当加在限位器上的荷载超过4.69kN时，限位器就会发生破坏。

2.3工况三：上部限位器正常工作，下部撑挡仅单侧处于正常工作状态

在上部限位器正常安装状态下，下部撑挡约束由于安装误差或使用磨损而可能导致某一侧撑挡失效，致使下部撑挡约束产生仅单侧处于正常工作的状态。在这种状态下，单边的撑挡约束是否能维持开启窗的安全稳定性，是工况三主要考察的问题。

分析在风荷载和重力作用下，上部限位器正常安装，下部右侧撑挡为单边正常工作状态时，整体模型约束处力的大小。通过计算可得，整体模型在下端右侧撑挡支撑杆及限位器的约束处产生的约束力见表4。

表4整体模型约束反力

反力位置

反力值/kN

上部限位器反力

11.07/0.47

右侧撑挡支撑杆Y向反力

2.07

右侧撑挡支撑杆Z向反力

3.43

由于下部撑挡单边正常工作，导致整体开启窗模型约束反力的不对称，故而上部两侧的限位器约束反力值出现不对称现象。

根据之前的结论可知，当限位器上施加的荷载超过4.69kN时，限位器就会发生破坏，而此时左侧限位器上所施加的荷载已经达到11.07kN，所以在该过程中左侧限位器最先破坏。当左侧限位器破坏后，开启窗模型仅剩右侧撑挡支撑杆与右侧限位器约束发挥作用，此时的约束反力值统计于表5。

表5左侧限位器破坏后约束反力

反力位置

反力值/kN

右侧限位器反力

0.57

右侧撑挡支撑杆Y向反力

2.75

右侧撑挡支撑杆Z向反力

4.55

当仅剩右侧撑挡与右侧限位器约束之后，对比工况一可知，此时撑挡约束上的力已然超过了撑挡破坏时所受的力，因此撑挡会随之发生破坏。之后仅留下右侧限位器，也很快发生破坏。因此最终的破坏顺序为左侧限位器最先破坏，进而导致右侧撑挡发生破坏，最终右侧限位器发生破坏，这便是整个工况三状态下开启窗模型的破坏顺序与机理。

基于上述三种工况下的计算分析结果，可以得出以下结论：首先，在进行限位器加固，且工作正常的情况下，由于限位器的约束作用，而使撑挡扇上部件和框上部件所受的荷载进一步减少，因此，提高了开启窗的安全性。其次，当下部撑挡失效或由于安装原因而无法正常工作。经计算发现，限位器底部边缘极易发生屈服破坏并产生塑性变形。最后，进一步计算发现，如果下部撑挡仅单侧处于正常工作状态，窗的约束都将发生破坏，从而使窗成为一个机构而有发生脱落的风险。

3 结论

对于挂钩式开启窗，五金系统的合理设计以及精确安装对于保证开启窗整体安全性十分重要。本文提出以下几方面建议：

1）对于既有玻璃幕墙开启窗，可额外装配防坠铰链，来提高开启窗整体安全性。

2）对于高度大于2m的挂钩式开启窗，可每边设置2对限位器，以防止发生开启窗脱钩并整体脱落的安全事故。

3）开启窗型材与五金件连接部位，应做局部加厚处理，同时选用优质紧固件，保证连接部位强度。

4）平时应加强开启窗维护保养，及时处理开启窗五金系统存在的质量问题。

作者李聪张喜臣

参考文献

[1]中国建筑科学研究院.JGJ102-2003玻璃幕墙工程技术规范[S].北京:中国建筑工业出版社,2003.

[2]中国建筑科学研究院.GB50009-2012建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.

[3]中国建筑金属协会.JGJ214-2010铝合金门窗工程技术规范[S].北京:中国建筑工业出版社,2010.

[4]中国建筑金属协会建筑门窗配套件委员会.JG/T126-2017建筑门窗五金件传动锁闭器[S].北京:中国建筑工业出版社,2017.